The Shape of Earth and Reference Ellipsoids

Elevation and the Ellipsoid

GPS receivers use a smoothed model of sea level to calculate elevation. The model is called a reference ellipsoid. This means that the elevation reading from the GPS receiver is not the vertical distance from true sea level, but rather the distance from the reference ellipsoid. In this tutorial, we introduce the concept of ellipsoids and reference ellipsoids in a way suitable for both teachers and students. Please use this and subsequent tutorials to help you learn more about accuracy, scientific models, and how GPS receivers work.

The Shape of the Earth: An Introduction to the Ellipsoid

The Earth is not a perfect sphere, but is instead more like a slightly squashed sphere called an ellipsoid. An ellipsoid looks like a basketball when someone is sitting on it. Instead of being perfectly round, it is squashed down from top to bottom, and bulged out from side to side. Because of mountains and valleys on Earth’s surface, the Earth isn’t a perfect ellipsoid either, but an ellipsoid is a good enough approximation of Earth’s overall shape.

The GPS Receiver and the Reference Ellipsoid Model

A GPS receiver gives latitude, longitude, and elevation. Let’s focus specifically on how a GPS receiver calculates elevation. The information required is:

1. The location of at least four satellites in space
2. The current time
3. The reference ellipsoidal shape of sea level for the entire Earth

There are many different reference ellipsoids, but all GPS receivers use the same one, and it is called the WGS-84 Reference Ellipsoid. Below is a picture of this ellipsoid with some lengths in meters for:

1. The distance from the North Pole to the Center
2. The distance from any point on the Equator to the Center

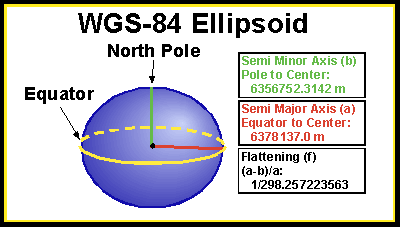
Notice that the Semi Major Axis (a) is LONGER than the Semi Minor Axis (b), Physically, this means the distance from side to side on the Earth is LONGER than from top to bottom, just like the squashed basketball. The lengths shown in the image define the exact shape of this ellipsoid, and are used by the GPS receiver to help it calculate elevation.

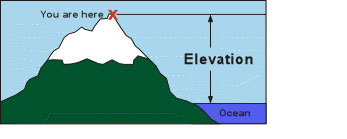
So, if a GPS receiver reports an elevation of 1600 meters, what that means is that you are 1600 meters above the reference ellipsoid.

Models and Their Usefulness in Science

The reference ellipsoid is a simplified model of the world around us. It is a smoothed mathematical representation of Earth’s sea level surface and ignores the effects of tides, seasonal currents, and waves. On land, the reference ellipsoid forms the mathematical surface that would be taken by sea level if the land areas were crisscrossed by canals. Why, then, would a model be useful in science? In the case presented here, a model (the reference ellipsoid) is helpful in measuring elevation because describing the true shape of sea level is complicated and would involved storing a lot of information within a GPS receiver.

Accuracy and Using Averages to Increase Accuracy

You may now be wondering, “If the GPS receiver is using a model that only approximates sea level to determine elevation, what effect does the shape of the reference ellipsoid have on an elevation measurement?” Usually this effect is expressed in terms of accuracy.

Since a GPS receiver uses the reference ellipsoid, and not true sea level, to calculate elevation, then the elevation measurement is sometimes less accurate. We say “sometimes,” because there are times when the reference ellipsoid matches true sea level.

How can you increase accuracy? Let’s say you took GPS measurements for a study site and you have taken 15 readings, 1 each minute for 15 minutes. As you did this exercise, the GPS readings probably seemed to wander, and so you used an average of all 15 measurements to get the position. This averaging increased the accuracy of your GPS coordinates from 100 meters to 30 meters.

Now we know the GPS receiver uses a model to figure out your elevation. To learn more about what using this model means about your elevation measurements, continue to the Geoid and GPS Receivers tutorial.